Ordinarily, we call the channels of communication and sensation modalities. We experience the world involving multiple modalities, such as vision, hearing or touch. A system which handles dataset includes multiple modalities is characterized as a multi-modality modal. For example, MSCOCO dataset contains not only the images, but also the language captions for each image. Utilizing such data, a model can learn to bridge the language and vision modalities.
In the latest decade, neural network architectures allow a system to process raw data automatically and
supply different levels of features representations. They have been widely applied to unsupervised
features learning for single modalities, which helps research to make progress connecting the computer
vision and natural language processing communities. A neural network-based multi-modality model learns
to map the distributed vectors of different modalities, from language to vision and from vision to
language. The model uses the predicted vectors which are based on the pairwise similarities to perform
retrieval or labeling, namely, the model learns to match the image representations and the text data, so
that we can obtain the corresponding images given a sentence query1.
However, integrating visual and language features is harder than one might expect, since these two modalities come not only with challenges of their own: their different semantic and representational nature make it hard to bring vision and language onto a common ground. One advantage of traditional features retrieval methods is that they require handcrafted patterns designed by domain expertise and their success or failures are interpretable. Because the features representations learned by neural networks are intransparent, thus the model itself can’t provide plausible explanation for the prediction. There is lacking strong evidence to explain whether such neural network-based models map the correct language features to the images or have just learned artifacts from the data.
The goal of this post is to investigate how a two-branch embedding network mapping image and text to a joint space. The approach used in this post is Layer-Wise Relevance Propagation (LRP)2. LRP is a popular interpretability approach in the field of explainable artificial intelligence. The basic rule of LRP is propagating the prediction scores backward through all the layers in the neural network until the input elements. We want to apply LRP to the two-branch embedding network to trace the pairwise similarities between the language and image vectors back to individual words.
LRP rules are nothing but the mathematical rules based on the forward operations in each layer, how these rules are designed are depending on the architectures of the layers. In the following sections, we will firstly get to know the embedding network and the important calculations in this network. After that, we will learn more about the LRP principles and their practical implementations based on the layer architectures of the embedding network. The implementations are detailed in each layer and supply clear trace about how the prediction scores are propagated back to each input token from the input layer. The input elements which are applied higher scores at the end are considered as relevant informations corresponding to the prediction result. In this way we can find out how the language source are mapped by the network to a given image. At the end, we obtain the evidence of the mapping results by investigating these relevant tokens.
Introduction of the embedding network
Wang et al. (2017)1 introduced two neural networks for solving image-text matching tasks. Each neural network has two branches to transform the features from two different modalities, i.e. image features and text features, and produce two different representations in the joint latent space where features of both modalities can be matched to each other through computing the distance or similarity between them. One of such neural networks, which will be investigated in this post, is referred to as Embedding Network, see the illustration of the architecture from Wang et al. (2017)1 in the following.
from IPython.display import Image
Image("img/EmbeddingNetwork.png",width = 300)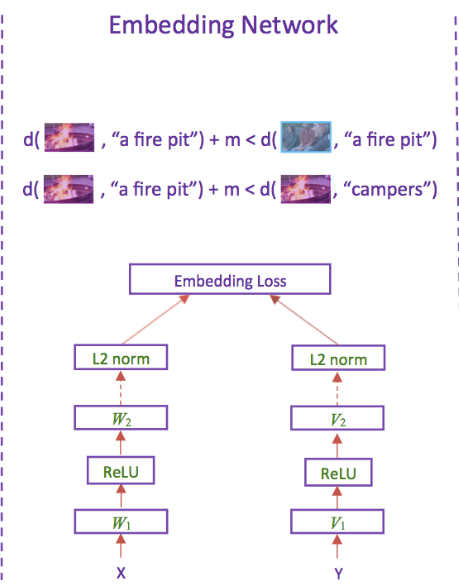
As it is shown in the figure, both branches in the network have the same architecture: each branch consists of two linear transformation layers with ReLU activation between them. The final layer outputs will be normalized by their L2 norm. The embedding loss states that the Embedding Network learns to reduce the distance between the transformed image and text features from positive image-text pairs and increase the distance between the negative pairs.
Wang et al. (2017)1
focused on investigating the behavior of the proposed two-branch networks, the
inputs X and Y are pre-computed features extracted from
other trained models, i.e. word embedding model for text features and image classification model for
image features. But let’s first have a view of the data to understand the difficulties of the task
before we get to the motivation of investigating the network.
Training and testing data
Wang et al. (2017)1 used the Flickr30K and MSCOCO datasets to train the two-branch networks. Both datasets supply multiple phrases or sentences to describe the same image or region. The embedding network is trained to not only match pairs of texts and images but also match the features within one modality, i.e., phrases or sentences for one image should also be close to each other after training and each of them have a similar distance to the same image.
Different to general classification tasks, the image-text matching system isn’t trained to predict a category of images or texts directly, but to search the nearest neighbor in the latent image-sentence embedding space through distance values between the text-image pairs. The labels of each dataset stand for the index of images and are used to construct positive and negative text-image pairs. For more details in testing on MSCOCO data, the accuracy is evaluated through computing a percentage of phrases or sentences for which the corresponding image is ranked among the chosen top matches.
Followings are two text-image pair examples from the MSCOCO test set, each image has 5 different captions.
Image("img/559101.jpg", width=300)
baby softly colorful padded chair , holding red plastic toy.
small kid chewing toy close sofa child toy cell phone mouth young child sitting car seat toy next
door. baby bouncy seat chewing plastic toy. Image("img/512787.jpg", width=300)
man wearing hat standing next fire station . person standing steep side walk next building . woman standing water bottle person wearing sunglasses hat standing street . man stands next brick building near stop sign city street .
Each image has multiple captions describing different things or scenes in the image. The Embedding Network is trained to map the embedded representations of image features and text features. In case of the image-sentence retrieval task: given a query image and the candidate sentences, to obtain the embed representations, we pass the image and text features through two branches of the network respectively. After that, we can compute the similarity scores (Euclidean distance in Wang et al. (2017)1 ) and rank the candidates in decreasing order. The correct match, e.g. the 5 corresponding captions of the image, should be on top of the ranking. As testing on the MSCOCO test set, the authors used the sentences to query images through ranking K similarity scores between the embedded representations and achieved the accuracy of 43.3% if K=1, 76.4% if K=5 and 87.5% if K=10. K stands for the number of the top matches.
The main work in this post
The aim of this post is to investigate which relevant tokens in one caption contributed the most in the sentence-image retrieval. From the above examples, we know that one image has five different captions. Each caption contains very different words or phrases describing different objects or regions in the image. Hence, the model isn’t learning to match one caption to one image directly, but different language features from one caption to its corresponding regions from the one image. Neither the above statistic results nor the similarity matrix between the latent representations of language and image features can explain for us which relevant features from different captions are actually matched to the given images. From a linguistic point of view, we should find out how the model really finds different key words to match the images. We need more explanation for the matching results of the network. In this post, we can try to apply the layer-wise relevance propagation approach to obtain the relevant tokens from the input space. Since the image features fed into the Embedding Network are extracted from a trained vision model, the relevance propagation beyond the Embedding Network is not the aim of this post and won’t be covered in the post and let’s only focus on the language side at this time.
Bach et al. (2015)2 introduced layer-wise relevance propagation (LRP) firstly for image classification to investigate the relevant features or regions from one image corresponding to the classified categories. Through the relevance propagation, the classification message can be traced back to the input features to explain the network decisions.
To date LRP is extended to natural language processing (Arras, Horn, Montavon, et al. 2016, 20173; Arras, Osman, et al. 20194 ) to extract relevant tokens in text classification. The major advantage of LRP is that it doesn’t require neural activation to be differentiable and we can linearly back propagate the relevance from layer to layer (Binder et al. 2016)5.
In the following parts of the post, we will go through the whole procedure starting from feature and model preparations which include obtaining the relevance. After that, we will learn how to implement the LRP algorithm for the architecture of the Embedding Network and redistribute the relevance onto the word embeddings. At the end, we need to visualize the relevance of each token to find the relevant tokens for the sentence-image matching result.
Preparing the trained model, sentence features and image features
Similarly to Wang et al. (2017)1,
I have trained the Embedding Network not from scratch but with pre-computed features. For running the
codes in this post to prepare the relevance propagation, please first download the repository liang/two-branch-netword_lrp for loading the trained models and importing
other required functions. The checkpoints of different models corresponding to different training data
are saved in directory models. And the language datasets and word embedding
features MT
GrOVLE can be found in directory data. If only for testing, it is not
necessary to download extra data or any other precomputed features. But you may still need to install
the prerequisites stated in the Readme file from the repository if requirements are not satisfied in
your python environment.
Load trained Embedding Network
Let’s first import the network and construct the configuration for loading the trained model. The
parameters of the trained model is saved in the file model_best.pth.tar. We just need
to reload the parameters to the network. Run model.eval() and the model is then
ready for computing the embedded representations for new input features.
from main import load_model, load_checkpoint
from main import Configs
import os
import torch
# names of trained models: attend, average
# names of datasets: coco, flickr
name = "average"
dataset = "coco"
# construct configurations for loading model and datasets
flags = Configs(name = name, dataset=dataset)
print(flags.name, flags.dataset)
# Load model framework and vocabulary
model,vocab_data = load_model(flags, image_feature_dim=2048)
# Load checkpoint
save_directory = os.path.join(flags.save_dir, flags.dataset, flags.name)
resume_filename = os.path.join(save_directory, 'model_best.pth.tar')
_, best_val = load_checkpoint(model, resume_filename)
# The two-branch-network contains the word embedding layer, text branch network and image branch network.
model.eval()Out[]:
average coco
args.language model average
embedding_dim, metric_dim: 2048 512
embedding_dim, metric_dim: 2048 512
Out[1]:
ImageSentenceEmbeddingNetwork(
(words): Embedding(16000, 300)
(word_reg): MSELoss()
(text_branch): EmbedBranch(
(fc1): Sequential(
(0): Linear(in_features=300, out_features=2048, bias=True)
(1): BatchNorm1d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Dropout(p=0.5, inplace=False)
)
(fc2): Linear(in_features=2048, out_features=512, bias=True)
)
(image_branch): EmbedBranch(
(fc1): Sequential(
(0): Linear(in_features=2048, out_features=2048, bias=True)
(1): BatchNorm1d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Dropout(p=0.5, inplace=False)
)
(fc2): Linear(in_features=2048, out_features=512, bias=True)
)
)
Both branches of the network have the same architecture: each branch starts with a linear transformation layer, which transforms the input features from two different modalities into a new representation with the same feature dimensions. Don’t forget that the output representation from each pass is first normalized by their L2 norm before that they are used to compute the Euclidean distance between two outputs.
Prepare sentence features
Sentence features will be prepared by the data loader, all tokens will be mapped to their indices in the vocabulary.
# sentence features for the first image and second image are the first 10 arrays from the test data set.
# Load test loader and extract the sentence features
from dataset_utils import DatasetLoader
test_loader = DatasetLoader(flags, 'test')
test_loader.build_vocab(vocab_data)
sent_features = torch.from_numpy(test_loader.sent_feats)[:10]
print(sent_features.size())Out[]: loading annotations into memory...
Done (t=0.46s)
creating index...
index created!
loading annotations into memory...
Done (t=0.29s) creating index...
index created!
torch.Size([10, 31])
Prepare image features
Let’s start with extracting the image features for the above samples. We can obtain the computed image features from the trained ResNet-152 model from torchvision.
# Image features
import cv2
import numpy
import torch
import torchvision
from torch.autograd import Variable
img_0 = cv2.imread('img/559101.jpg')
img_0 = cv2.resize(img_0,(224,224))
img_1 = cv2.imread("img/512787.jpg")
img_1 = cv2.resize(img_1,(224,224))
img = numpy.array([img_0,img_1 ])[...,::-1]/255.0
mean = torch.Tensor([0.485, 0.456, 0.406]).reshape(1,-1,1,1)
std = torch.Tensor([0.229, 0.224, 0.225]).reshape(1,-1,1,1)
img_feats = (torch.FloatTensor(img.transpose([0,3,1,2])*1) - mean) / std
img_feats.size()Out[]: torch.Size([2, 3, 224, 224])
Load the trained ResNet152 model and feed the initial features of the given images to the network to compute image features representations.
ResNet = torchvision.models.resnet152(pretrained=True);ResNet.eval()Check the computed features of the network for the given images through returning the classification results. The first ten predicted object categories will be shown in order to have an interpretation about what the extracted features may represent.
# utils script contains the 1000 image classes from vision model
import utils
results = ResNet(img_feats)
print(results.size())
scores = numpy.array(results.data)
ranking = numpy.argsort(-scores)
for j in range(2):
print("Classified result of image {}".format(j))
for i in ranking[j][:10]:
print('%50s (%3d): %6.3f'%(utils.imgclasses[i][:50],i,scores[j][i]))torch.Size([2, 1000])
Classified result of image 0
pajama, pyjama, pj's, jammies (697): 13.331
ice lolly, lolly, lollipop, popsicle (929): 13.102
spatula (813): 12.005
Band Aid (419): 10.371
wooden spoon (910): 10.233
bib (443): 9.681
Christmas stocking (496): 9.471
nipple (680): 9.174
toilet seat (861): 9.059
harmonica, mouth organ, harp, mouth harp (593): 8.753
Classified result of image 1
street sign (919): 8.431
traffic light, traffic signal, stoplight (920): 8.274
pay-phone, pay-station (707): 8.076
parking meter (704): 7.382
trench coat (869): 6.909
unicycle, monocycle (880): 6.882
crane (517): 6.450
cash machine, cash dispenser, automated teller mac (480): 6.211
cab, hack, taxi, taxicab (468): 6.153
scale, weighing machine (778): 6.070
Although the architecture of ResNet152 won’t be detailed in this post, but we can easily decompose the network for obtaining layer outputs from specific layers or modules.
names = list(ResNet._modules.keys())
print("Modules in ResNet152: ", names)
# Collect the modules before the output layer
modules = [ResNet._modules[k] for k in names[:-1]]
X = [img_feats] + [None] * (len(modules))
for i,m in enumerate(modules):
X[i+1]=(m.forward(X[i]))Modules in ResNet152: ['conv1', 'bn1', 'relu', 'maxpool', 'layer1', 'layer2', 'layer3', 'layer4', 'avgpool', 'fc']
At the end, we can extract the output from the average pool layer before the last output layer from the network as image features representation.
image_features = X[-1].reshape(2, 2048)
print(image_features.size())torch.Size([2, 2048])
Compute embedded representations and obtain relevance
After the image and text features for the above two examples are prepared and the trained parameters are loaded into the model, we can project the text and image features into one joint latent space through two branches of the network and compute the multiplication between two representations at the end. The similarity scores can be considered as relevance which can be propagated back to the input features. According to the redistribution rules of LRP, the elements from the input which are relevant to the similarity result should receive high relevance (Bach et al. 2015)2 .
Firstly we can decompose each branch of the Embedding Network and extract all the layers from each branch to obtain the output of each layer.
Text branch
#Extact layers from the modules dictionary.
layers_text_branch = [layer for key,layer in model._modules["text_branch"]._modules["fc1"]._modules.items()]
layers_text_branch.append(model._modules["text_branch"]._modules["fc2"])Since the Embedding Network receives one feature vector for each sentence as input representation, we can’t feed the text branch with the sequence directly but we need to firstly compute an average value of the embedding features of each token by the length of the sentence and summarize the values of all tokens in one sentence to obtain a sentence vector. The sentence representation has as a result the same dimension as the word embedding size.
# In text branch, we don't feed the model with word embedding features directly.
# Instead, we have to compute an average embedding for each sequence.
# Retrieve the embedding layer from the model
layer_embedding = model._modules["words"]
# Embeddings has dimensions of (sequences_num, sequence_length, embedding_dim)
embeddings = layer_embedding(sent_features)
# number of words (exclude the pad tokens)
n_words = torch.sum(sent_features > 0, 1).float() + 1e-10
sum_embeddings = embeddings.sum(1).squeeze()
# Compute an average of each sequence as sentence embedding
sentences = sum_embeddings / n_words.unsqueeze(1)Now we can collect the layer outputs for the text branch layer by layer in the forward direction where we feed the output from the lower layer to the higher connective layer as input. The output of the last layer will be normalized by its L2 norm.
activations_text = [sentences] + [None] * len(layers_text_branch)
for i,l in enumerate(layers_text_branch):
activations_text[i+1] = layers_text_branch[i].forward(activations_text[i])
print(activations_text[i+1].size())
text_feats_normalized = torch.nn.functional.normalize(activations_text[-1])torch.Size([10, 2048])
torch.Size([10, 2048])
torch.Size([10, 2048])
torch.Size([10, 2048])
torch.Size([10, 512])Image branch
We have obtained the image features from the average pooling layer from ResNet-152, there is no further preprocessing step necessary. We can feed the features of the above images directly to the image branch of the network.
layers_image_branch = [layer for key,layer in model._modules["image_branch"]._modules["fc1"]._modules.items()]
layers_image_branch.append(model._modules["image_branch"]._modules["fc2"])# Now we can evaluate the layer inputs for image branch in the forward direction
activations_image = [image_features] + [None] * len(layers_image_branch)
for i,l in enumerate(layers_image_branch):
activations_image[i+1] = layers_image_branch[i].forward(activations_image[i])
print(activations_image[i+1].size())
img_feats_normalized = torch.nn.functional.normalize(activations_image[-1])torch.Size([2, 2048])
torch.Size([2, 2048])
torch.Size([2, 2048])
torch.Size([2, 2048])
torch.Size([2, 512])We can validate the last layer outputs from both decomposed text and image branches with the outputs computed by the model, to check if all the layers are linearly connected.
im_feats, text_feats= model(image_features, sent_features)
print(torch.all(im_feats.eq(img_feats_normalized)))
print(torch.all(text_feats.eq(text_feats_normalized)))tensor(True)
tensor(True)At last, we have to compute the similarity scores which indicate the matching results between the given sentence-image pairs.
The Euclidean distance between the normalized representations
The Euclidean distance between \(\mathbf{p}\) ( img_feats_normalized) and \(\mathbf{p}\) (text_feats_normalized) is obtained through: \(\left| \mathbf{q} - \mathbf{p} \right| = \sqrt{ \left| \mathbf{p} \right|^2 + \left| \mathbf{q} \right| ^2 - 2 \mathbf{p}\cdot\mathbf{q}}\). Since both text and image features representations are normalized by their L2 norm, \(\left| \mathbf{p} \right|^2\) and \(\left| \mathbf{q} \right|^2\) are equal to 1, as a result, \(\left| \mathbf{q} - \mathbf{p} \right| = \sqrt{ 2 - 2 \mathbf{p}\cdot\mathbf{q}}\)
The larger the product of \(\mathbf{p}\cdot\mathbf{q}\), the smaller the distance between \(\mathbf{q}\) and \(\mathbf{p}\) is, the better the model has learned to match the texts representation to the images in the embedding space. Hence, we can consider the multiplication of \(\mathbf{p}\cdot\mathbf{q}\) as the relevance representing the text-image matches.
scores = torch.mm(text_feats_normalized, img_feats_normalized.transpose(0, 1))Obtain the relevance to be propagated
The positive image-text pairs are the first 5 captions and first image, the last 5 captions and the second image. By multiplying the similarity scores by the label mask we can obtain the relevance for the sentence features given the corresponding image.
mask_0 = torch.FloatTensor([1.,0.]).unsqueeze(0)
mask_1 = torch.FloatTensor([0.,1.]).unsqueeze(0)
mask_0.size(), mask_1.size()(torch.Size([1, 2]), torch.Size([1, 2]))relevance_0 = scores * mask_0
relevance_1 = scores * mask_1print(relevance_0)
print(relevance_1)tensor([[0.5763, 0.0000],
[0.7036, 0.0000],
[0.6464, 0.0000],
[0.6017, 0.0000],
[0.6467, 0.0000],
[0.4672, 0.0000],
[0.3577, 0.0000],
[0.4364, 0.0000],
[0.4462, 0.0000],
[0.4151, 0.0000]], grad_fn=<MulBackward0>)
tensor([[0.0000, 0.5462],
[0.0000, 0.5320],
[0.0000, 0.5096],
[0.0000, 0.4412],
[0.0000, 0.5910],
[0.0000, 0.4230],
[0.0000, 0.4213],
[0.0000, 0.5028],
[0.0000, 0.3981],
[0.0000, 0.2716]], grad_fn=<MulBackward0>)In order to obtain the relevance for the pass of text branch, we still need to map the above relevance to the normalized representation. Since the L2 norm doesn’t change the proportion of contribution, we can apply this computed relevance for the text branch directly to the last layer output, that is the relevance we will propagate through the branch.
text_relevance_0 = torch.sum(text_feats_normalized.unsqueeze(-1) * (relevance_0.unsqueeze(1)/img_feats_normalized.transpose(0,1).unsqueeze(0)),-1)
text_relevance_1 = torch.sum(text_feats_normalized.unsqueeze(-1) * (relevance_1.unsqueeze(1)/img_feats_normalized.transpose(0,1).unsqueeze(0)), -1)print(text_relevance_0.size())
print(text_relevance_1.size())torch.Size([10, 512])
torch.Size([10, 512])Now, we have finished the forward computation procedure. We have extracted the outputs of each layer from the network, obtained two relevance vectors corresponding to two different images for the text representations. In the following section, we will learn how to propagate these relevances back to the word embeddings features, so that we can investigate which tokens are relevant to the matching results between the captions and the given image.
Layer-wise relevance propagation
In order to understand the process of the relevance propagation in the following sections, let’s firstly clarify the general principle of LRP, which is to redistribute the relevance messages from the top layer back to the lower layers until the input features. Suggest there are two connective layers, and neuron output \(Z_j = \sum_i Z_{ij}\), \(i\) is the number of neurons from the lower layer and \(j\) is the number of neurons of the higher layer. Each neuron of the lower layer receives relevance redistributed from the relevance of the higher layer according to it’s contribution in the forward computation and written as: $$R_i^{l} = \sum_j Z_{ij}\frac{R_j^{(l+1)}}{ Z_j }$$
It is possible for \(Z_j\) to be equal or close to zero and the relevance will explode. In this case, we can modify the redistribution rule with a stabilizer \(\epsilon\), e.g.: \(R_i^{l} = \sum_j Z_{ij}\frac{R_j^{(l+1)}}{ Z_j + \epsilon}\), where if \(Z_j \lt 0 \) then \(Z_j - \epsilon\).
According to the original paper (Bach et al. 2015)2 , the exact propagation rule depends on the architecture of the network. Because of different computation in different layer, the propagation algorithm varies from layer to layer. In the forward computation of each branch in the Embedding Network, we have seen the sequential model consists of different modules as follows: Linear, BatchNorm1d, ReLu, Dropout, followed by a Linear layer at the end. Because of the different properties of different layers, we need to define different rules for different layers accordingly. The main components which contain learning parameters in Embedding Network are the linear layers and the batch normalization layers. The propagation rules in these layers depend on the message pass in the forward computation, which will be detailed below. In the activation layer and dropout layer there is no mixing of inputs to compute outputs and the dimensions of input and output is identical, hence in these layers, we can define \(R^{(l)} = R^{(l+1)}\).
Linear layer
In the forward computation, neuron output \(Z_j\) is computed through multiplying input \(a_i\) with the connective weights \(w_{ij}\) from the layer: $$Z_{j} = \sum_{i}a_i w_{ij}$$
The relevance propagation rule can be defined as dividing the relevance by the output of each neuron \(Z_j\) and redistribute them back to the input \(a_i\), \(a_i\) is the neuron output from the lower layer: $$R_i = \sum_k \frac{a_i w_{ij}}{\epsilon + \sum_{i} a_i w_{ij}} R_j$$
Implementation in numpy:
def Linear_LRP(R, layer, layer_input, layer_output):
weights = layer.weight.detach().numpy().T
eps = 1e-6
sign_out = numpy.where(layer_output>=0,1.0,-1.0)
eps = eps * sign_out
denom = layer_output + eps
part = numpy.expand_dims(weights,0) * numpy.expand_dims(R/(denom), 1)
R = layer_input * (part.sum(axis=-1))
return R Batch normalization layer
Decompose the computation in forward direction Ioffe, Sergey, and Christian Szegedy. 20156:
- mini batch mean: \(\mu_{\mathcal B} \leftarrow \frac1m \sum_{i = 1}^m x_i\)
- mini batch variance: \(\sigma_B^2 \leftarrow \frac{1}{m} \sum_{i=1}^{m}(x_i - \mu_B)^2\)
- normalize: \(\hat{x_i} \leftarrow \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\)
- scale and shift: \(y_i \leftarrow \gamma \hat{x_i} + \beta \equiv \mbox{BN}_{\gamma,\beta}(x_i)\)
Where \(\gamma\) and \(\beta\) are the learning parameters.
Step rules of propagating the relevance to the input in batch normalization layer according to Lapuschkin (2018):
- relevance in scale and shift: \(R_{\hat{x_i}} = \gamma\hat{x_i}\frac{R^{l+1}}{y_i}; R_{\beta} = \beta\frac{R^{l+1}}{y_i}\)
- relevance in normalize: \(R_{(x_i -\mu_B)} = R_{\gamma\hat{x_i}}\)
- relevance in batch variance: \(R^{(l)} = x_i\frac{R_{(x_i -\mu_B)}}{(x_i -\mu_B)}; R_{\mu_B} = \mu_B\frac{R_{(x_i -\mu_B)}}{(x_i -\mu_B)}\)
A compiled expression for the relevance backward pass for input \(x_i\) yields $$R^{(l)} = \frac {x_i \cdot \gamma\hat{x_i} \cdot R^{l+1}}{(x_i -\mu_B) \cdot y_i} = \frac {x_i \cdot \gamma \cdot R^{(l+1)}}{\sqrt{\sigma_B^2 + \epsilon} \cdot y_i}$$
Implementation in numpy:
def BatchNorm_LRP(R, layer, layer_input,layer_output):
weights = layer.weight.detach().numpy().T
eps = layer.eps
mean = layer.running_mean.detach().numpy()
var = layer.running_var.detach().numpy()
denom = (numpy.sqrt(var)) * layer_output + eps
part = numpy.expand_dims(weights,0) * numpy.expand_dims(R/(denom), 1)
R = layer_input * (part.sum(axis=-1))
return R# Sequence of layers in the text branch
print(layers_text_branch)[Linear(in_features=300, out_features=2048, bias=True), BatchNorm1d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True), ReLU(inplace=True), Dropout(p=0.5, inplace=False), Linear(in_features=2048, out_features=512, bias=True)]Propagate the relevance from layer to layer
# This propagation algorithm is designed specific for the text branch in the Embedding Network.
def LRP_EmbeddingNetwork(R, As, branch):
Rs = [None] * len(branch) + [R]
for i in range(0,len(branch))[::-1]:
layer = branch[i]
if i == 0 or i == 4:
Rs[i] = Linear_LRP(Rs[i+1], layer, As[i], As[i+1])
if i == 1:
Rs[i] = BatchNorm_LRP(Rs[i+1], layer, As[i], As[i+1])
if i == 2 or i == 3:
Rs[i] = Rs[i+1]
return RsInitialize the collection of relevance and detach all tensors from the computation graph of the model for convenience.
As = [output.detach().numpy() for output in activations_text]Propagate the text relevance from the output layer back to the input layer for each image separately. Relevance in the input layer are the relevance on the sentence vectors.
Rs_0 = LRP_EmbeddingNetwork(text_relevance_0.detach().numpy(), As, layers_text_branch)
sent_relevance_0 = Rs_0[0]Rs_1 = LRP_EmbeddingNetwork(text_relevance_1.detach().numpy(), As, layers_text_branch)
sent_relevance_1 = Rs_1[0]Each sentence vector contains the average values of the embedding features of all the tokens in one sentence. As following, we should allocate the sentence relevances to each token.
sum_output= As[0] * n_words.unsqueeze(1).detach().numpy()
avg_input = embeddings.detach().numpy()
avg_input = avg_input/sum_output[:,numpy.newaxis,:]
R_embed_0 = avg_input * sent_relevance_0[:,numpy.newaxis,:]
R_embed_1 = avg_input * sent_relevance_1[:,numpy.newaxis,:]Obtain word-level relevance
So far, we have redistribute the relevance onto word embedding vector in the input space. Arras et al. (2016)3 suggested to pool the relevance over all embedding elements of each token to obtain the word-level relevance scores in their task for explaining text classification through finding the word-level relevant features . $$R_w = \sum_i R_{iw}$$
R_embed_0 = R_embed_0.sum(axis=-1)
R_embed_1 = R_embed_1.sum(axis=-1)
print(R_embed_0.shape)(10, 31)Word-level relevance visualization and discussion
In this post, we have just propagated the relevance in the text branch. As it is mentioned in the beginning, the relevance propagation for the image branch involves further propagation in the vision model, which is not covered in this post. But we can investigate the token relevance since the visualization of each individual token according their score values supplies evidence of the matching results of the Embedding Network. In order to compare the word level relevance to the image relevant features, we can use the image classification results as reference, because the classification results show that what the image features are representing.
As it is mentioned above, sentence-image retrieval is different to classification. We obtain the
relevance from the similarity scores, hence, we will investigate the relevant features of all captions
given one image, not just the positive ones. In order to obtain the word-level visualization for the
example captions in HTML format please check the heatmap functions in the utils file and
import the assisting function html_table and return the HTML table which is the
visualization of relevant tokens.
The retrieval score is basically the very first relevance from the matching results. The higher the score, the more confident the network matches the caption to the given image. The following word-level relevances represent that, tokens highlighted in red are the positive matches to the given image, in blue then on the opposite side. The color opacity is computed through normalization with the maximum and minimum absolute relevance scores in each sentence following the instruction from (Arras, et al., 2016)3 .
captions = test_loader.captions[:10]from utils import html_table
print(html_table(captions,R_embed_0, relevance_0[:,0].detach().numpy()))print(html_table(captions,R_embed_1, relevance_1[:,1].detach().numpy()))Image("img/559101.jpg",width=300)
Classified result:
pajama, pyjama, pj's, jammies (697): 13.331
ice lolly, lolly, lollipop, popsicle (929): 13.102
spatula (813): 12.005
Band Aid (419): 10.371
wooden spoon (910): 10.233
bib (443): 9.681
Christmas stocking (496): 9.471
nipple (680): 9.174
toilet seat (861): 9.059
harmonica, mouth organ, harp, mouth harp (593): 8.753| Retrieval score: 0.576 | baby | softly | colorful | padded | chair | , | holding | red | plastic | toy | . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Retrieval score: 0.703 | small | kid | chewing | toy | |||||||
| Retrieval score: 0.646 | close | ofa | child | toy | cell | phone | mouth | ||||
| Retrieval score: 0.601 | young | child | sitting | car | seat | toy | next | door | . | ||
| Retrieval score: 0.646 | baby | bouncy | seat | chewing | plastic | toy | . | ||||
| Retrieval score: 0.467 | man | wearing | hat | standing | next | fire | station | . | |||
| Retrieval score: 0.357 | person | standing | steep | side | walk | next | building | . | |||
| Retrieval score: 0.436 | woman | standing | water | bottle | |||||||
| Retrieval score: 0.446 | person | wearing | sunglasses | hat | standing | street | . | ||||
| Retrieval score: 0.415 | man | stands | next | brick | building | near | stop | sign | city | street | . |
The matching scores have shown us that the best match for the first image is the second caption, and the relevance visualization provides us with the evidence for the score with the highlighted tokens: red represents positive relevance while blue means negative. For example, the second caption received the highest matched score. The only found relevant token “toy” from this caption is the only reason for this result.
When we look at the five captions of the first image, different captions describe different objects and scenarios in the image. As a result, we find different relevant features in each caption: ‘softly’,’close’,’young’,’bouncy’. The results have also shown us that the relevant features from the text are discrete. The text branch of the Embedding Network didn’t capture the dependency information of the sequence, namely, it is challenging for the model to map image features to complete phrases.
Image("img/512787.jpg",width=300)
Classified result:
street sign (919): 8.431
traffic light, traffic signal, stoplight (920): 8.274
pay-phone, pay-station (707): 8.076
parking meter (704): 7.382
trench coat (869): 6.909
unicycle, monocycle (880): 6.882
crane (517): 6.450
cash machine, cash dispenser, automated teller (480): 6.211
cab, hack, taxi, taxicab (468): 6.153
scale, weighing machine (778): 6.070| Retrieval score: 0.546 | baby | softly | colorful | padded | chair | , | holding | red | plastic | toy | . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Retrieval score: 0.532 | small | kid | chewing | toy | |||||||
| Retrieval score: 0.509 | close | ofa | child | toy | cell | phone | mouth | ||||
| Retrieval score: 0.441 | young | child | sitting | car | seat | toy | next | door | . | ||
| Retrieval score: 0.591 | baby | bouncy | seat | chewing | plastic | toy | . | ||||
| Retrieval score: 0.422 | man | wearing | hat | standing | next | fire | station | . | |||
| Retrieval score: 0.421 | person | standing | steep | side | walk | next | building | . | |||
| Retrieval score: 0.502 | woman | standing | water | bottle | |||||||
| Retrieval score: 0.398 | person | wearing | sunglasses | hat | standing | street | . | ||||
| Retrieval score: 0.271 | man | stands | next | brick | building | near | stop | sign | city | street | . |
The above visualization shows the results based on the second image. The last five sentences are corresponding captions. The similarity scores indicate further challenges of the task. The Embedding Network matches discrete features from language to images. Not only images are paired with multiple captions but also features from captions can be applied to different images.
The first five captions of the first image obtained higher similarity scores than the correct captions. And the most relevant tokens from the wrong captions are “toy” given the second image. From the correct captions, tokens like “sign” “street” “station” are identified as significant features. There are complicated semantic features in the second image that the model failed to capture.
Of course, it is difficult to look into every example and find out specific patterns from the language side to explain the sentence-image matching results. But from the relevance result, we can obtain a more intuitive view about why the model succeeds or fails.
There are several possible quantitative analysis methods to validate the relevant tokens or using the relevance for evaluating the working of the network depending on the task and data. For example, if we have marked phrases annotated in the data set, we will be able to calculate the overlaps between the annotated key phrases and the found relevant tokens. Or we can move out the negative tokens (in blue) and just keep the positive relevant tokens in the captions and execute the testing process to validate the relevant tokens. If the matching results don’t change much then we can verify that we found the relevant tokens.
Take-home message
In this post, we have applied the layer-wise relevance propagation approach for explaining the network results using the relevant tokens as evidence. We go through the whole procedure about how to compute the layer outputs of both branches in the Embedding Network, obtain the relevance to be propagated and at the end propagate the relevance to the word embedding features. From the identified relevant tokens based on an image, we found that the network has troubles to map image features to whole phrases and fails to align the evident objects from the image to the strong relevant text as we expect. As for the first image, the text ‘toy’ rather than ‘child’ or ‘baby’ gained more focus given an image showing a baby mainly. These relevance achieved by the layer-wise relevance propagation validate the problems of the training data in this field: there are many captions containing the general subject words like “child”, “man” or “woman” and thus many are coming up during training as a negative example. As a result, more unique and distinguishing objects, like “toy” are considered as the important information for the network to make decisions. The results shown in the post have suggested that the Embedding Network solves the image retrieval problem by exploiting shallow patterns in the data rather than complete phrases.
Yet, this post has just supplied a practical instruction about applying the method, we still need further statistical analysis based on the identified relevant features for clearer explanations about the working of the network.
- Wang,Liwei, Yin Li, Jing Huang, Svetlana Lazebnik. “Learning Two-Branch Neural Networks for Image-Text Matching Tasks,” in CoRR, 2017
- Bach, Sebastian et al. (July 2015). “On Pixel-Wise Explanations for Non-Linear Classifier Decisions by Layer-Wise Relevance Propagation”. In: PLoS ONE 10.7. doi: 10.1371/journal.pone.0130140. url: http://dx.doi.org/10.1371%2Fjournal.pone.0130140
- Arras, Leila, Franziska Horn, Gregoire Montavon, et al. (2016). “Explaining Predictions of Non-Linear Classifiers in NLP”. In: Proceedings of the 1st Workshop on Representation Learning for NLP. Association for Computational Linguistics.
- Arras, Leila, Ahmed Osman, et al. (2019). “Evaluating Recurrent Neural Net-work Explanations”. In: Proceedings of the ACL’19 Workshop on Black-box NLP. Association for Computational Linguistics.
- Binder, Alexander et al. (Jan. 2016). “Layer-Wise Relevance Propagation for Deep Neural Network Architectures”. In: isbn: 978-981-10-0556-5. doi:10.1007/978-981-10-0557-2_87.
- Sergey Ioffe and Christian Szegedy. “Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift,” in CoRR, 2015




